Algorithm Notation Difference

Algorithm Notation Difference. Mathematical notation to write algorithms. And latin american countries todos:

PPT Algorithm Complexity & BigO Notation From the from www.slideserve.com

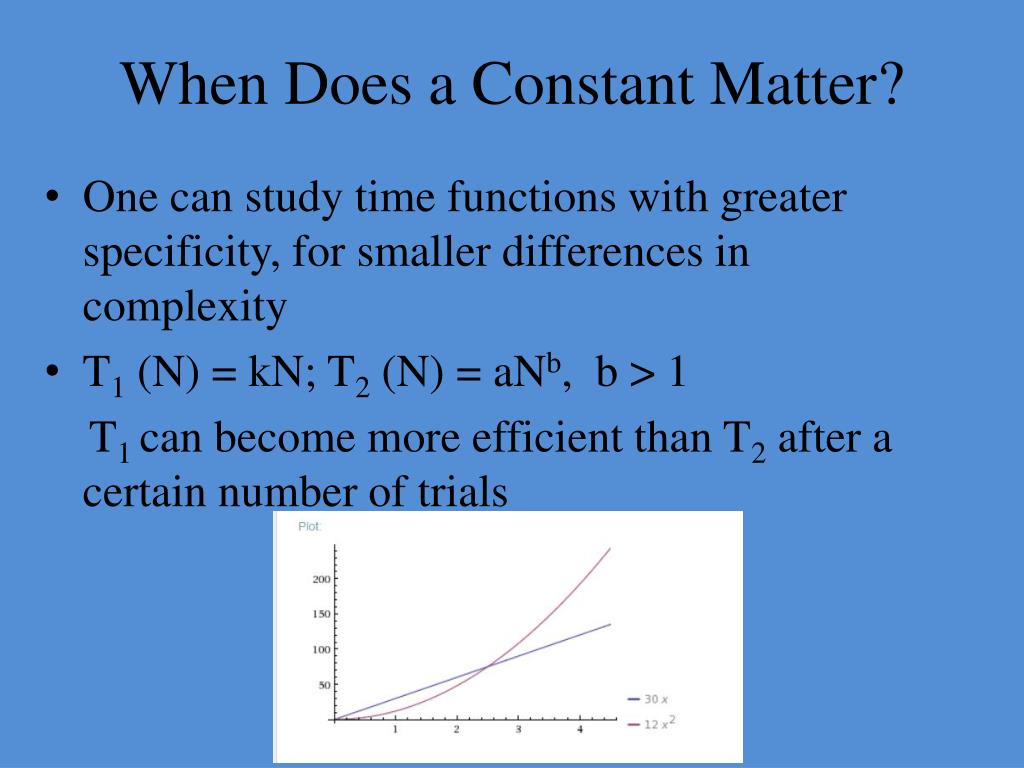
It’s like <= versus <. For example, if an algorithm runs in the order of n2, replacing n by cn means the algorithm runs in the order of c2n2, and the big o notation ignores the constant c2. F(x)<= o(n^2) big omega is like >=, meaning the rate of growth is greater than or equal to a specified value, e.g:

Source: www.slideserve.com

Big omega is used for the best case analysis of an algorithm. The quadratic formula is an algorithm, because it is a method for solving quadratic equations.

Source: droidtechknow.com

Big o notation is used for the worst case analysis of an algorithm. This can be written as c2n2 = o (n2).

Source: www.slideserve.com

For example, if an algorithm runs in the order of n2, replacing n by cn means the algorithm runs in the order of c2n2, and the big o notation ignores the constant c2. As later calculator models were introduced, the emphasis on rpn gradually diminished.

Algorithms Generally Have The Following Characteristics:

Some of the lists of common computing times of algorithms in order of performance are as follows: Ω ( f (n)) ≥ { g (n) : For example, if an algorithm runs in the order of n2, replacing n by cn means the algorithm runs in the order of c2n2, and the big o notation ignores the constant c2.

As Later Calculator Models Were Introduced, The Emphasis On Rpn Gradually Diminished.

As you progress through this tutorial, you will see some differences between space and. Big o is like <=, meaning the rate of growth of an algorithm is less than or equal to a specific value, e.g: In very simple language difference would be like this:

Notation Name O(1) Constant O(Log(N)) Logarithmic O((Log(N))C) Polylogarithmic O(N) Linear O(N2) Quadratic O(Nc) Polynomial O(Cn) Exponential Note That O(Nc) And O(Cn) Are Very Different.

Mathematical notation comparisons between u.s. Algorithms may not even involve math, but formulas almost exclusively use numbers. The hp35 manual had an appendix devoted to explaining the rpn algorithm.

It Tells Us That A Certain Function Will Never Exceed A Specified Time For Any Value Of Input N.

F (n) is o (g (n)) if there exist positive constant c and n0 such that. But it’s an upper bound of the case it depicts. The slower growing functions are listed first.

There Exists C > 0 And N.

This can be written as c2n2 = o (n2). The key difference between algorithm and flowchart is that an algorithm is a step by step procedure to solve a given problem while flowchart is a diagram that is used to represent an algorithm. For example, we know that the worst case time of quick sort is o ( n 2 ) , which means there exists a constant c for sufficiently large n, so that the time consumed by worst cases of quick sort is bounded by c n 2.