Grover's Algorithm Time Complexity

Grover's Algorithm Time Complexity. Square root time complexity means that the algorithm requires o (n^ (1/2)) evaluations where the size of input is n. Grover’s algorithm solves oracles that add a negative phase to the solution states.

Let's build a quantum computer! from pt.slideshare.net

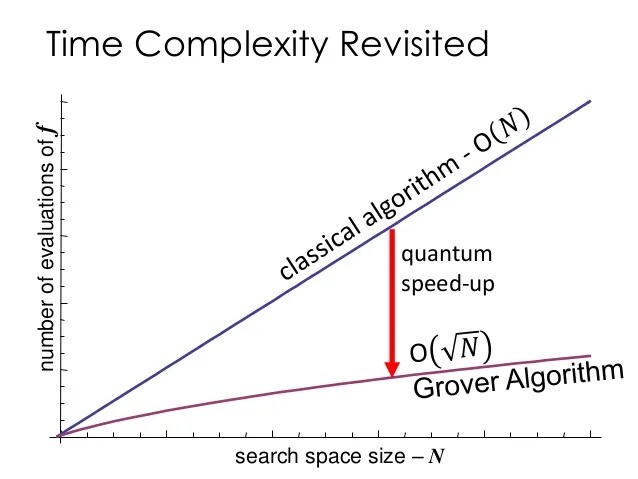
I have read that grover's algorithm has a complexity of o [n^0.5], or the square root of n. This is optimal in the sense that a lower bound to the time complexity for this problem was shown to be w(p Trying to understand grover's algorithm.

Source: pt.slideshare.net

Grover’s algorithm solves oracles that add a negative phase to the solution states. The present letter proposes a modification in the well known grover’s search algorithm, which searches a database of n unsorted items in o(√n/m) steps, where m represents the number of solutions to the search problem.

Source: lvee.org

This requires additional space but. It seems clear to me that it is $\omega(\log(n) \sqrt{n})$ since there are $\omega(\sqrt{n})$ iterations and each iteration requires use of the reflection operation which in turn takes time $\omega(\log(n))$ using any standard set of universal gates.

Source: quantumcomputing.stackexchange.com

Concurrency control techniques and extra registers for marking and storing the solutions are used in the modified algorithm. To me, this seems less efficient than a regular binary search, which has a time complexity of o [lg (n)], or log base 2 of n.

This Is The Main Reason To Apply Grover's Algorithm To The Searching Problem.

Show activity on this post. • 8x/2 l, a(x) outputs 0. As a result, in 1996, grover formulated an optimal quantum algorithm for the unstructured search problem.

But Is The Performance Of The Algorithm Any Good?

Time algorithm, we could, given nvariables arranged in clauses, solve the sat problem by searching all 2 npossibilities in o(log(2 )) = o(n) queries after a few manipulations. This oracle will be a diagonal matrix, where the entry that correspond to the marked item will have a. In addition, grover’s algorithm uses only o(p

There Exists A Randomized Algorithm A(X) Running In

For any state | x in the computational basis: This is one of the examples of immediate ways to combine quantum search with the rho method as mentioned in [ 3 ]. Trying to understand grover's algorithm.

3.3 Complexity In A Classical Search Algorithm, You Expect To Nd Tafter N 2 Iterations On Average, Which Is O(N).

Classically, you need to make boolean query for n/2 (average) times and in worst case for n times. Concurrency control techniques and extra registers for marking and storing the solutions are used in the modified algorithm. Let’s look at the time complexity that we’ve managed to achieve.

What Is The Time Complexity (Not Query Complexity) Of Grover's Algorithm?

I have read that grover's algorithm has a complexity of o [n^0.5], or the square root of n. Therefore, it provides a quadratic speedup over its classical counterparts. Grover’s search algorithm searches a database of n unsorted items in o(√n/m) steps where m represents the number of solutions to the search problem.