Algorithm With Notation
Algorithm With Notation. The latter grows much, much faster, no Linear search in best o(1), in worst o(n).
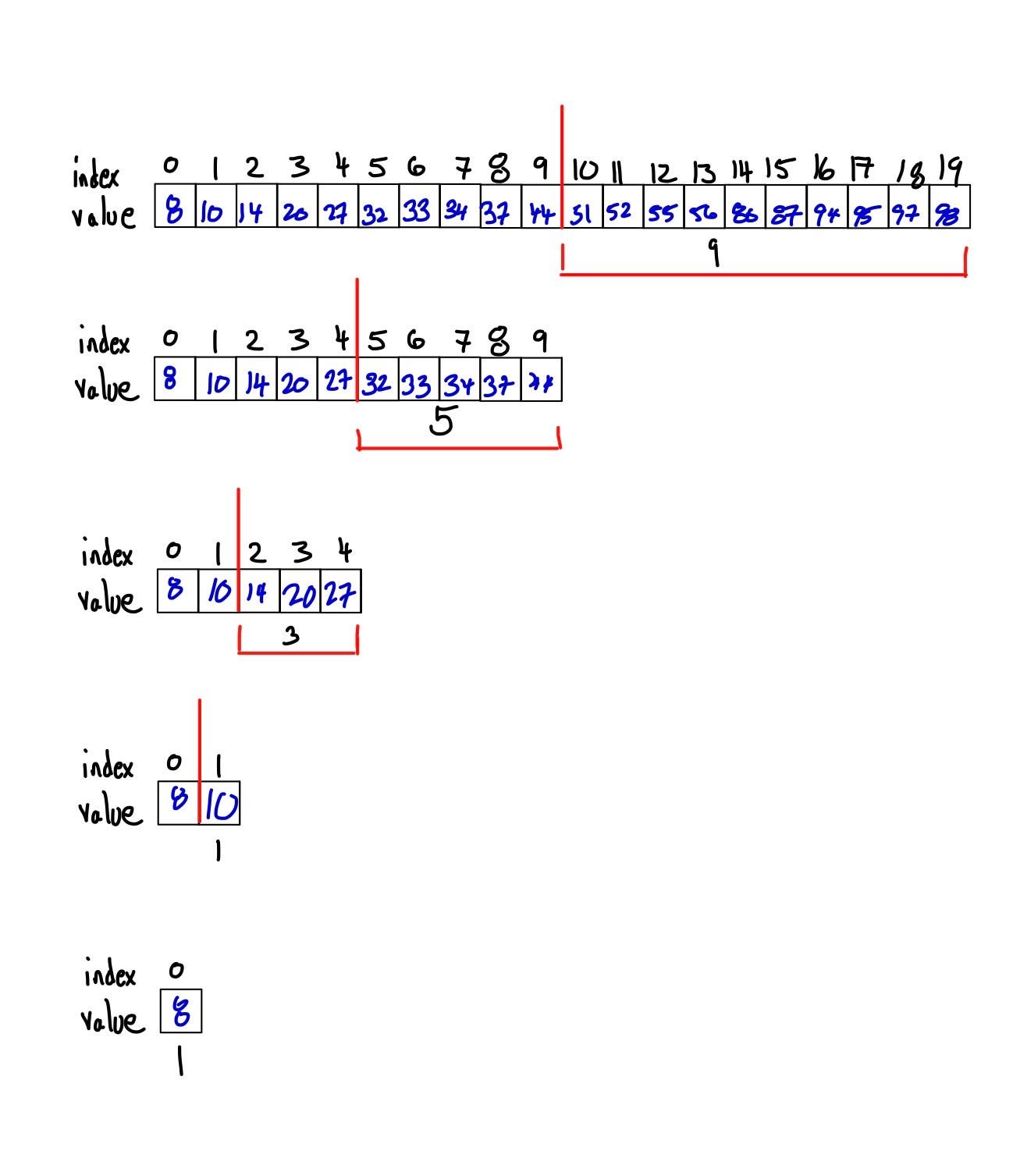
Items in the sequence are index by a variable such as i, j, k as a subscript. Let's consider some hypothetical algorithms for sorting a list of numbers. The big o notation is useful when we only have an upper bound on the time complexity of an algorithm.
The Notation Itself Is Simple, Consisting Of The Letter O Followed By A Formula Enclosed In Parentheses.
Many haskell statements can be translated directly into mathematical notation. Because we all know one thing that finding a solution to a problem is not enough but solving that problem in the minimum time/space possible is also necessary. This is just like array notation.
C Is Some Arbitrary Constant.
Then we say that f = o (g) if and only if f (n)/g (n) is bounded when n approaches infinity. There exist positive constant c and n0 such that 0 ≤ c g (n) ≤ f (n), for all n ≥ n0} Notation name o(1) constant o(log(n)) logarithmic o((log(n))c) polylogarithmic o(n) linear o(n2) quadratic o(nc) polynomial o(cn) exponential note that o(nc) and o(cn) are very different.
How To Calculate Big O — The Basics.
Big o notation describes how an algorithm's estimated runtime increases when we increase the size of the problem we are solving. There exist positive constants c and n0 such that 0. A key to reading notation for sequences is the notation of indexing elements in the sequence.
If It's Truly Important To Describe The Algorithm In Mathematical Notation, Look To Haskell For Inspiration.
Items in the sequence are index by a variable such as i, j, k as a subscript. Let's consider some hypothetical algorithms for sorting a list of numbers. The big o notation is useful when we only have an upper bound on the time complexity of an algorithm.
Often The Notation Will Specify The Beginning And End Of The Sequence, Such As 1 To N, Where N Will Be The Extent Or Length Of The Sequence.
How many steps an algorithm takes; The notation was proposed by the german mathematician paul bachmann in 1892 before the development of computers. With such a notation, it's easy to compare different algorithms because the notation tells clearly how the algorithm scales when input size increases.
Komentar
Posting Komentar